THURSDAY, 13 MAY 2021
The year of 1970 was unusually sunny in the UK, albeit quite tumultuous around the world. The Beatles had just announced their separation, the Brazilian soccer team won its third World Cup, and bicycles were finally permitted across San Francisco's Golden Gate bridge. Also, the US invaded Cambodia, expanding the reach of the Vietnam War, the Apollo 13 mission had failed, and episodes of political violence were increasing in Northern Ireland. But in a place that oftentimes seems to be far away from the rest of the world, in a remarkably untidy office in the middle of the calm city of Cambridge, John Horton Conway was fiddling with a GO board and a computer. He would ultimately invent the rules of what is perhaps his most famous invention: the Game of Life.This year, the Game of Life, one of the most well known mathematical games of the century, turns 50 years old. It seems only fitting, during this 50 year special edition of BlueSci, to then celebrate the magnum opus of one of Britain’s most eminent mathematicians. Although, in all honesty, I have the feeling that if Professor Conway heard me call the Game of Life his “magnum opus”, he would throw a book at my head. And he would be absolutely right.
Through numerical games, mathematical teasers, and the unabridged curiosity of an insatiable mind, Conway proved and disproved a myriad of mathematical claims and theorems. Peeking into his achievements is similar to following the white rabbit into the proverbial hole in the ground. Among his contributions to mathematics, we find many mathematical games of great relevance in the fields of combinatorial game theory, number theory, and recreational mathematics. He invented sprouts, an addictive game where each player takes turns connecting dots by lines that never cross each other. The game ends when it becomes impossible to draw a line that will not cross another. He also created phutball, short for philosophers football - as a matter of fact, he came up with dozens of games, which can be found in his book Winning Ways for your Mathematical Plays. He discovered a new category of numbers, the surreals, a set of numbers that includes all that are infinitely big, and infinitely small. He designed a new notation, useful to write down particularly big numbers. He created a whole new algebraic structure - a group - that carries his name. Down the rabbit hole, we are greeted by a Doomsday algorithm, and we find a curious zoo of mathematical creatures, such as quaternions, octonions, and even a huge monster.
It was however the Game of Life that, despite Conway’s eye rolling and fist clenching, catapulted him to fame, making him well known by people outside of his field of expertise. It all started with a column written by a friend of Conway’s, Martin Garden, for the magazine Scientific American. Before the internet was even a thing, Conway and Life went viral - it is speculated that there was a time in the 1970s when the game was played in a quarter of the world’s computers, making it the most coded game in history.
The rules of Life are hauntingly simple. Starting with a two dimensional grid, where each space may harbor a living cell at a time, the game evolves as follows: if the cell has less than two neighbours, it dies of loneliness. If it has more than four, it dies of overcrowdedness. Otherwise, it survives to live happily to the next round of the game. Finally, a cell may be born in an empty space, if that space has exactly three living neighbours.
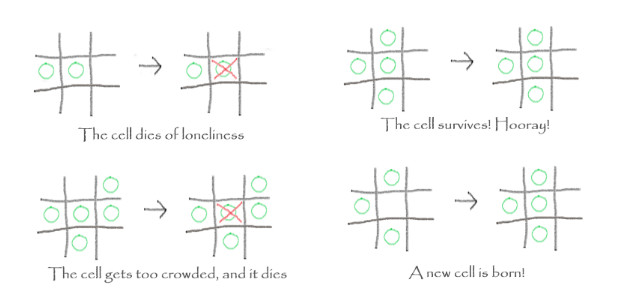
Each round of the game is called a generation. The rules are applied in all spaces simultaneously, and cells survive, die, and are reborn following Conway’s four commandments. The algorithm runs again and again. In this game with no players, all you have to do is set the initial configuration, and then sit down and watch it unfold. Some patterns eventually completely disappear, leaving behind a cold, lifeless, grill-shaped universe. Others are random or repeat themselves for all eternity.
Beyond the beautifully hypnotic patterns, its playful nature, and the simplicity of its rules, Life has a remarkably complex outcome. To begin with, the game has a property known as undecidability: there is no way to predict if an arbitrary configuration of cells will live on, or if they are eventually doomed to extinction. It is also a universal model of computation, meaning it is a very powerful data analysis tool. Perhaps more importantly, it also means that with enough cells and a big enough grid the game can actually simulate, and it is therefore equivalent to, any computer. Any results, mathematical curiosities, theorems, and postulates that can be proven true in the Game of Life can potentially be extended to results that hold true for entire areas of study in computer science.
The game also fuels a discussion that roots in very fundamental aspects of physics, ignited by a deceptively silly question: is Life alive? What kind of complex patterns could potentially emerge if we had an infinitely large grid, and no time limits? And what does that tell us about free will and our own reality? Many years after he created Life, Conway together with Canadian mathematician Simon Kochen postulated the so-called free-will theorem, where it is stipulated that if we, as observers of reality, have free will - meaning that our actions are not determined by a past configuration - then, under certain assumptions, elementary particles must have free will too.
Life is an example of a larger class of mathematical models called cellular automatons. While these models were proposed initially during the 1940’s, Conway was the one who, through Life, popularized them among mathematicians, computer scientists, physicists, biologists, academics, and non-academics alike. The field of research involving cellular automatons exploded, and applications were found aplenty. These automatons can be developed to simulate and predict physical, biological, chemical, ecological, social, political, computational, and medical phenomena, to name a few. They have even been used to create art and music.
It is very hard to quantify the impact Life has had, and continues to have, both inside and outside the academic community. Being a particularly simple case of the larger group of cellular automatons, Life provides a great toy model on which to test different hypotheses. In Arxiv, the biggest online repository of academic pre-prints, hardly a week goes by without a new article being posted analyzing the countless facets of the game. Outside of the secluded world of academia, Life sparked a somewhat cult following: there is even an entire wiki, LifeWiki, devoted to the game.
Conway was a great mathematician. Beyond his contributions to the field, he had the rare and admirable ability of being able to burst the bubble of academia and reach out to the public. He did this by illustrating complex mathematical concepts via games and word plays. He did not particularly like the attention that Life received, and he definitely did not consider it his biggest achievement. In Conway’s opinion, Life didn't have any interesting consequences, and he presumably gave it very little thought in his later years. When asked during an interview what he would like to know before he died, Life did not cross his mind. He answered: “I’d like to know why does the monster exists”. He passed away this year in April, three days after contracting COVID-19. He never found out why the monster exists - or if he did, he never told us. But that is a story for another time.
Maria Julia Maristany is a 1st year PhD student in Physics at Robinson College. Artwork by Eva Pillai
